• Tweet

相関関係の意味とは

皆さんこんにちは。コミュニケーション講座を開催している公認心理師の川島達史です。今回は心理学の視点をベースにした「相関関係」について解説していきます。

目次は以下の通りです。

①相関関係とは何か
②提唱者と歴史
③相関関係と因果関係の違い
④散布図で理解を深める
⑤練習問題で理解

是非最後までご一読ください。

 

①相関関係とは何か

意味

相関関係は心理学辞典（1990）[1]によると

2つの変数間の相互関係を表す指標

と定義されています。上記の定義には3つのキーワードが入っています

・2つ
相関関係は2つの関係を見る指標です。

・変数
変数とは、変わる数字という意味です。2つの変数はお互い変化することを意味しています。

・相互関係
相互関係とは、お互いが影響し合うという意味になります。よく因果関係と対比されますが、因果関係が一方通行で主従関係があるのに対して、相関関係は相互に影響し合うフラットな関係なのです。

 

具体例

例えば、細田・田嶌（2009）[2]の研究では以下の結果が得られました。

上図は、「自己肯定感」と「他者肯定感」は相互にプラスの影響があるということを表しています。すなわち自己肯定感が高くなると、他者肯定感を持ちやすくなり、逆もまた同じように言えると解釈することができます。

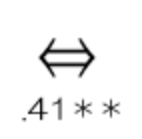
＊＊の意味

中央にある数字には「**」という印がついています。これは、ざっくりと統計的に意味のある結果が出たことを表しています。すなわち「**」があるということは、統計的なお墨付きが出たということになるので、心理的な主張をしたい時に引用することができます。無印の場合は、根拠としては弱いので気をつけましょう。

数字の強さ

次に数字を見ていきましょう。これは、専門用語で「相関係数」といいます。相関の強さはの一般的な目安としては、以下のようになります。

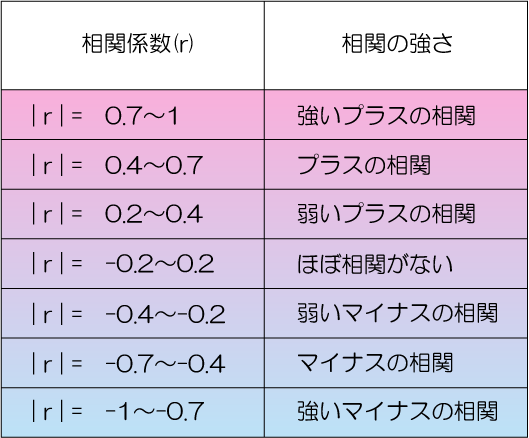
先程挙げた「.41**」の数字は、中程度のプラスの相関であることがわかります。相関係数が大きいほど主張の裏付けとしての確度が上がるので必ずチェックするようにしましょう。

②提唱者と歴史

相関関係は以下の３人の学者によって提唱されました。

1.オーギュスト・ブラヴェ

相関関係を提唱したのは、フランスの物理学者オーギュスト・ブラフェです。1844年に相関の統計的概念に関する論文を発表し、初めて相関関係の定義を発表しました[3]。

2.フランシス・ゴルトン

イギリスの人類学者、統計学者、初期の遺伝学者であるフランシス・ゴルトンは、相関の統計的概念を作成し、平均回帰を広く推進しました。ゴルドンはダーウィンの進化論の影響を受け、心的遺伝に興味を持ちました。そこから人間能力の研究、優生学や相関研究を含む統計的研究法を発達させました[4]。

3.カール・ピアソン

イギリスの統計学者カール・ピアソンは、1901年、ウェルドンとゴルトンと共に、彼は統計理論の発展を目的としたジャーナルBiometrikaを設立した[5]。「相関関係」は、正式には「ピアソンの積率相関関係数」と呼びます。

③相関関係と因果関係の違い

相関関係と似たことばに因果関係という言葉があります。この２つの違いを知っておくことで、相関関係の理解が深まります。

相関関係の読み取り方

相関関係は、お互いに影響し合う関係でした。例えば、スマホ利用時間が増えれば、アプリダウンロード数も増えますし、ダウンロード数が増えればスマホ利用時間も増えることが考えられます。この場合は、２つは相互に影響し合っているため「相関関係」にあると言えます。

 

因果関係の読み取り方

因果関係は「一方通行」の関係を意味します。例えば、気温が上がれば扇風機の売上は増えますが、扇風機の売上が上がっても、気温は上昇しません。つまり、この関係は一方通行で、「因果関係」にあると言えます。このように、一方的に影響を与えている関係を「因果関係」があると言います。

 

④散布図で理解を深める

相関関係は「プラスの相関」「マイナスの相関」「無相関」の３つの基準があります。これをパッと見で判断できるのが、「散布図」と呼ばれるグラフです。それぞれ解説していきます。以下の図をご覧ください。まずはプラスの相関から見ていきましょう。

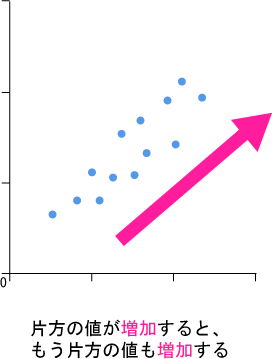
このように、「右肩上がり」に散布される図は、１つが大きくなると他方も大きくなるプラスの相関にあると、読み取れます。続いて、マイナスの相関はどうでしょうか。

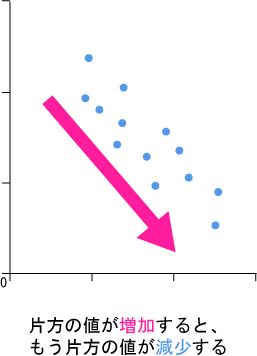
こちらは、プラスの相関とは逆に「右肩下がり」に散布されています。一方が大きくなると、他方が少なくなります。最後に無相関を見ていきましょう。

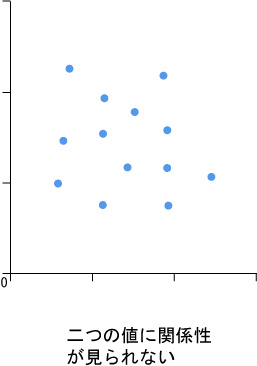
２つの軸の間に一定の傾向が見られずに、バラつきがあります。こうした結果となった場合、「無相関」であると読み取れます。

このように、相関関係を視覚的に理解するために、グラフを用いる場合があります。数字だけではなくグラフ化した場合、どのような傾向が現れるのか知識として備えておきましょう。

 

⑤練習問題で理解

最後に練習問題で理解を深めていきましょう。

練習問題１

上図は齋藤ら（2008）の研究です[6]。相関関係、因果関係のどちらを表していますか。また、相関の強さはどのぐらいでしょうか。

 

解答
相互に影響し合っているので相関関係にあると言えます。－の表記がないので正の相関関係にあたります。相関の強さとしては、0.4～0.7に該当するため、中程度となります。

 

練習問題２

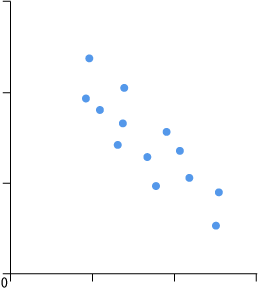
上記のグラフは、「プラスの相関」「マイナスの相関」「無相関」のうち、どれに該当するでしょうか。

 

＊解答例
右肩下がりなので、マイナスの相関と読み取ることができます。

ダイコミュ用語集監修